Mathematik in verschiedenen Bereichen – ein Projekt der JS2 im Schuljahr 2024 / 2025
Elf Schülerinnen und Schüler des Mathematikkurses der Jahrgangsstufe 2 im erhöhten Anforderungsniveau von Frau Wellmann haben sich mit verschiedenen spannenden Themen beschäftigt, die im Alltag der Menschen eine Rolle spielen und in denen Mathematik eine zentrale Bedeutung hat.
Die Endergebnisse des Projekts sind unten aufgeführt.
Wie erklärt man Vektoren im dreidimensionalen Raum?
Diese Frage habe ich mir gestellt – und als Antwort kam mir die Idee, ein Modell zu entwickeln, mit dem man das Thema spielerisch und anschaulich vermitteln kann. Denn: Was man einmal selbst in der Hand hatte und gesehen hat, versteht man meist besser.
Ich begann damit, eine stabile Basis aus Pappe zu bauen, auf der ein dreidimensionales Koordinatensystem Platz finden sollte. Dieses Koordinatensystem habe ich ebenfalls aus Pappe gefertigt. Doch schnell wurde mir klar: Ein Koordinatensystem allein reicht nicht aus, um Vektoren wirklich verständlich zu erklären. Denn zu Vektoren gehören auch Punkte im Raum – und natürlich die Vektoren selbst, die diese Punkte mit dem Ursprung verbinden.
Um das greifbar zu machen, habe ich mit Schaschlikspießen, einem Faden und einer Holzkugel gearbeitet. Die Spieße ermöglichen es, Punkte auch in der dritten Dimension (x₃-Richtung, also nach oben) zu realisieren. Die Holzkugel symbolisiert einen Punkt im Raum. Sie ist mit einem Faden verbunden, der durch ein Loch im Koordinatenursprung geführt ist. Am unteren Ende ist der Faden auf eine Spule gewickelt, sodass man ihn herausziehen und anschließend wieder aufrollen kann. Durch ein Loch in der Kugel lässt sich diese auf einen Schaschlikspieß stecken, sodass eine feste Position im Raum entsteht.
Zwischen dem Ursprung und der Kugel entsteht nun eine gerade Verbindung – der Faden bildet also einen anschaulichen Vektor. Auf diese Weise lässt sich sehr einfach erklären, was ein Vektor ist: eine gerichtete Strecke vom Ursprung zu einem Punkt im Raum.
Um aus dem Modell schließlich eine vollständige Lernstation zu machen, habe ich noch ein Arbeitsblatt erstellt. Es enthält Aufgaben, die die Lernenden Schritt für Schritt an das Thema heranführen und sie mit dem Modell arbeiten lassen. So entsteht ein interaktiver Zugang zum abstrakten Thema “Vektoren im dreidimensionalen Raum”, der nicht nur verständlich, sondern auch motivierend ist.
Pia Müller
Altersbestimmung von Fossilien mit Hilfe von Mathematik
Im Rahmen meines Mathematikprojekts habe ich mich mit Fossilien beschäftigt – genauer gesagt damit, wie man ihr Alter mithilfe von mathematischen Methoden bestimmen kann. Ich habe dieses Thema gewählt, weil ich mich in letzter Zeit sehr für die Entstehung der Erde, der Menschheit und deren zeitliche Einordnung interessiere. Durch die Altersbestimmung von Fossilien, die oft sehr selten und wertvoll sind, kommen wir unserem Ziel näher, zu verstehen, wann welche Lebewesen gelebt haben und wie sich das Leben auf der Erde entwickelt hat.
Um solche Erkenntnisse zu gewinnen, spielt die Mathematik eine zentrale Rolle. Mithilfe mathematischer Methoden zur Altersbestimmung können wir Zeiträume von Tausenden bis hin zu Milliarden Jahren zurückverfolgen. Es gibt verschiedene Verfahren, mit denen das Alter von Fossilien oder Gesteinen bestimmt werden kann – darunter die Radiokarbonmethode (C14-Methode), die Kalium-Argon-Methode und die Uran-Blei-Methode.
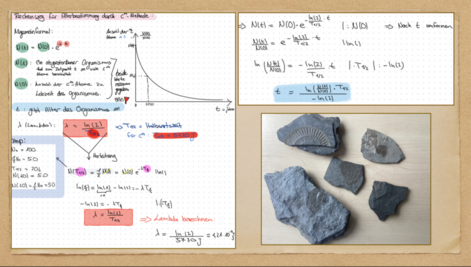
In meinem Projekt habe ich mich besonders auf die C14-Methode konzentriert. Diese Methode basiert auf dem radioaktiven Zerfall des Kohlenstoff-Isotops C14, das in lebenden Organismen vorhanden ist. Sobald ein Lebewesen stirbt, nimmt es kein C14 mehr auf, und das vorhandene C14 beginnt mit einer bekannten Halbwertszeit von etwa 5730 Jahren zu zerfallen.
Ich habe mich mit der Frage beschäftigt: Wie funktioniert die Altersbestimmung von Fossilien mit Hilfe von Mathematik? Dabei habe ich auch untersucht, was ein C14-Isotop ist und wie es entsteht. Ein zentraler Teil meiner Arbeit war die Auseinandersetzung mit der mathematischen Formel und ihrer Herleitung. Insgesamt hat mir das Projekt gezeigt, wie faszinierend und wichtig mathematische Modelle in der realen Forschung sein können – besonders in Bereichen wie der Archäologie, Geologie oder Paläontologie.
Rana Abdi
Matheschwäche bei Kindern im Grundschulalter
In meinem Projekt habe ich mich damit beschäftigt, wie man Kindern im Grundschulalter mit Matheschwäche so helfen kann, dass sie im Unterricht mitkommen und auch im Alltag weniger Probleme haben.
Begonnen habe ich mein Projekt mit einer „Checkliste“ für Eltern, anhand derer sie die Probleme ihrer Kinder, mit denen eines Betroffenen vergleichen können. Wenn andere diese Liste durchlesen, bekommen sie ein besseres Verständnis welche Schwierigkeiten Kindern mit Dyskalkulie (= Matheschwäche) haben.
Der nächste Schritt war die Erstellung eines Lerntherapieplans, der beschreibt, wie man die Schwierigkeiten der Kinder gezielt angehen kann. Der Plan enthält die Ziele der Lerntherapie – von der Förderung des Zahlenverständnisses und der Einführung von Rechenstrategien bis hin zur Stärkung von Selbstständigkeit und Selbstvertrauen. Zudem beschreibt er den zeitlichen Ablauf der Therapie sowie die Inhalte, einschließlich des eingesetzten Materials.
Für das Material habe ich mir zwei Spiele überlegt. Das erste Spiel ist ein Mathe-Memory. Dafür habe ich (wie bei einem herkömmlichen Memory) Karten erstellt, bei denen jeweils zwei zusammengehören, allerdings mit Matheaufgaben. Zum Beispiel steht auf einer Karte „15 : 3“ und auf der passenden Karte „5“. So wird Mathe spielerisch gelernt, und die Schwierigkeit kann je nach Leistungsstand des Kindes angepasst werden. Das Spiel kann beliebig oft wiederholt werden, wodurch sich die Lösungen der Rechnungen einprägen. Das Kind muss im Unterricht dann nicht mehr lange überlegen.
Ein weiteres Spiel ist das „Pizza-Spiel“. Die Idee dazu kam mir, weil mir selbst als Kind Brüche wie ⅛ mithilfe von Pizzastücken erklärt wurden. Bei diesem Spiel belegt das Kind eine Pizza – die Aufgabenstellung kann dabei variieren. Zum Beispiel: „Ich möchte zwei Stücke Salami und zwei Stücke Mozzarella.“ Nachdem das Kind die entsprechenden Stücke auf die Pizza gelegt hat, kann man fragen: „Wie viele Stücke sind jetzt insgesamt auf der Pizza?“ Durch die visuelle Darstellung fällt es dem Kind leichter, die Rechenaufgabe nachzuvollziehen. Das Tolle an diesem Spiel ist, dass es sich nicht wie Rechnen anfühlt und keine direkt sichtbaren Zahlen enthält. Viele betroffene Kinder zeigen nämlich eine Ablehnung gegenüber Mathematik oder Zahlen. So wird eine positive Verbindung zum Rechnen hergestellt.
Amelie Ehmsen
Wie schwierig dürfen logische Reihen für die Klassenstufen sein?
Im Rahmen unseres Matheprojekts habe ich mich mit logischen Reihen beschäftigt. Ich war schon immer an logischen Reihen interessiert und konnte in diesem Projekt meiner Kreativität freien Lauf lassen, da logische Reihen sehr vielfältig sind. Sie fördern unser logisches Denken und unsere Gedächtnisleistung, wodurch wir lernen, gezielter zu analysieren und bessere Schlussfolgerungen zu ziehen.
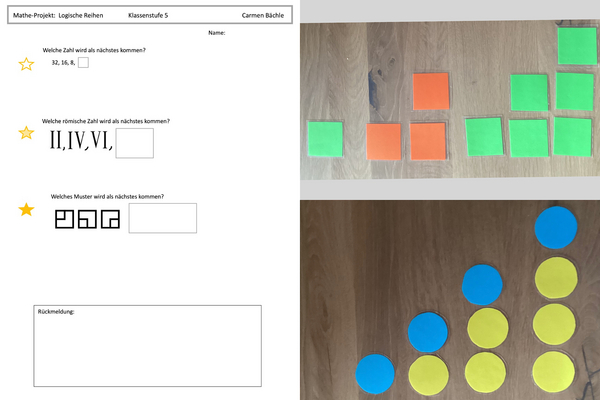
Damit jede Klassenstufe von 1 bis 13 mit diesen Aufgaben lernen kann, habe ich für jede Jahrgangsstufe ein eigenes Arbeitsblatt erstellt. Jedes Arbeitsblatt enthält drei Schwierigkeitsgrade sowie eine Beispielaufgabe, die durch viele weitere Aufgaben mit ähnlichem Schwierigkeitsgrad ergänzt werden können. So kann das Material flexibel im Unterricht oder zur individuellen Förderung eingesetzt werden. Die Arbeitsblätter habe ich alle getestet und überarbeitet, damit der Schwierigkeitsgrad so optimal, wie möglich ist.
Viele dieser Aufgaben lassen sich auch ins Analoge übertragen, z.B.: die Muster. Muster sind eine beliebte Form von logischen Reihen und besonders für jüngere Schülerinnen und Schüler gut geeignet. Um die Aufgaben anschaulicher zu gestalten, können beispielsweise Plättchen oder andere Materialien verwendet werden, bei den hinzugekommenen Elemente farblich hervorgehoben werden.
Für ältere Schüler lassen sich die Aufgaben komplexer gestalten – zum Beispiel mit mathematischen Inhalten wie Vektoren, die im Bildungsplan vorgesehen sind. So lässt sich das Thema altersgerecht differenzieren und sinnvoll in den Unterricht integrieren.
Insgesamt hat mir das Projekt gezeigt, wie vielfältig und kreativ Mathematik sein kann. Es hat mir großen Spaß gemacht, ein Thema zu bearbeiten, das nicht nur Denkvermögen fördert, sondern auch spielerische und praktische Zugänge zur Mathematik ermöglicht.
Carmen Bächle
Insulin Dosierung im Alltag bei Diabetes mellitus Typ 1
In meiner Projektarbeit im Mathe eAN-Kurs habe ich mich mit dem Thema „Insulin Dosierung im Alltag bei Diabetes mellitus Typ 1“ beschäftigt. Ziel war es, wie man mithilfe mathematischer Formeln die notwendige Menge an Insulin für einen Typ-1-Diabetiker berechnen kann, und warum diese exakte Berechnung im Alltag lebenswichtig ist.
Zu Beginn habe ich den medizinischen Hintergrund zu Diabetes mellitus Typ 1 kurz erklärt. Dabei handelt es sich um eine Autoimmunerkrankung, bei der die Bauchspeicheldrüse kein Insulin mehr produziert. Menschen mit dieser Erkrankung müssen Insulin von außen zuführen, und zwar in genau der Menge, die ihrem aktuellen Blutzuckerspiegel und der aufgenommenen Menge an Kohlenhydraten entspricht.
Im mathematischen Teil der Arbeit habe ich die grundlegende Formel zur Insulinberechnung vorgestellt und anhand konkreter Werte erklärt:
Benötigte Insulineinheiten = (BE × BE-Faktor) + (aktueller Blutzucker – Zielwert) / individuelle Insulinresistenz
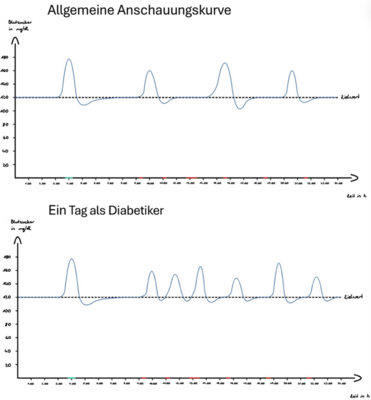
Ein zentrales Element von meinem Projekt war eine allgemeine Blutzuckerkurve eines Typ-1-Diabetikers, bei der man gut erkennen konnte, wie sich der Blutzuckerspiegel über den Tag verändert – abhängig vom Essen und der Insulineinnahme. Als zusätzlichen Schritt habe ich auch ein simuliertes Tagesprofil erstellt, wie es bei mir persönlich aussehen würde, wenn ich Diabetiker wäre. Dabei habe ich echte Werte für Mahlzeiten, Blutzucker und Insulinmenge ermittelt, vereinfacht und den Verlauf grafisch dargestellt. Das hat gezeigt, wie individuell und anpassungsbedürftig die Therapie sein muss. Dadurch wird auch sichtbar, dass jeder Diabetiker eine eigene Berechnung braucht, um seinen Blutzucker zu regulieren, da viele Faktoren eine Rolle spielen und diese bei jedem Individuell sind.
Jannis Lapp
Mathematische Modellierung des E. Coli-Wachstums unter verschiedenen Umweltbedingungen
Mit meiner Ausarbeitung möchte ich die verschieden Wachstumskurven von E. Coli Bakterien darstellen, wenn man diese unter verschiedenen Bedingungen wachsen lässt. Ich habe fünf verschiedene Umgebungsbedingungen im Vergleich zur Optimal Bedingung für deren Wachstum ausgesucht, darunter die Temperatur, den pH-Wert, das Sauerstoffangebot und das Nährstoffangebot. Mit der gleichen Anfangszellzahl wurden alle verschiedenen Ansätze in einem gleichen Zeitraum kultiviert und deren Wachstum alle zwei Stunden dokumentiert. Die Daten wurden dann zuerst in eine Wachstumsrate verrechnet und danach in eine Exponentialfunktion. Die unterschiedlichen Funktionen wurden dann mit dem Graph der Funktion für das optimale Wachstum verglichen und geschaut, um welchen Faktor sich diese zueinander unterscheiden.
Tiago Anthonj
Wie TikTok & Instagram-Algorithmen arbeiten – und warum
Ich habe mich für dieses Thema entschieden, weil ich selbst oft TikTok und Instagram nutze und mir aufgefallen ist, wie gut die Inhalte zu meinen Interessen passen. Das hat mich neugierig gemacht: Wie funktioniert das eigentlich – und was hat das mit Mathematik zu tun?
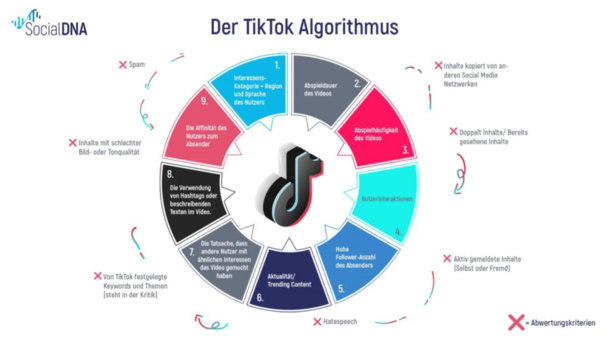
Im Unterricht wurde deutlich: Hinter diesen Algorithmen steckt vor allem Mathematik – z. B. Datenanalyse, Wahrscheinlichkeiten und Vektoren. TikTok bewertet, wie du mit Videos umgehst (z. B. wie lange du sie
anschaust, ob du likest oder kommentierst). Daraus erstellt der Algorithmus ein Interessenprofil und zeigt dir gezielt passende Inhalte.
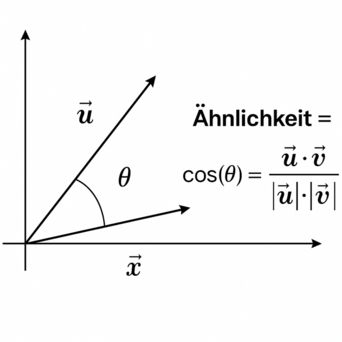
Instagram funktioniert ähnlich, bezieht aber zusätzlich dein Netzwerk (z. B. Freunde, Interaktionen) stärker mit ein. Mathematisch werden Nutzer*innen und Videos als sogenannte Vektoren dargestellt – also als Zahlenreihen, die Interessen und Eigenschaften beschreiben. Der Algorithmus vergleicht, wie ähnlich sich diese Vektoren sind: Je ähnlicher, desto eher wird dir das Video angezeigt. Diese Ähnlichkeit wird mit dem Winkel zwischen den Vektoren berechnet (Cosinus-Funktion).
Vorteile: Du bekommst genau die Inhalte, die dich interessieren. Die Plattform lernt schnell und liefert passende Vorschläge. Nachteile: Es entstehen Filterblasen, kritische Inhalte werden oft ausgeblendet, und
es besteht Sucht- sowie Datenschutzgefahr.
Quelle zum Bild: cdn.prod.website-files.com/6601491bd4f34ae35a9dfb57/66c5f2c5c08051e7e7ac3ec4_661d02cf9009ed54dc3805d8_SDNA-Blogbeitrag-TikTok-Algorithmus-1536x864.webp
Louis Denne
Wie reise ich klimafreundlich? - Mathematischer Vergleich des CO2-Ausstoßes verschiedener Verkehrsmittel
Im Rahmen unseres Matheprojekts, habe ich mich mit dem aktuellen Thema Umwelt und Reisen
beschäftigt und mit welchem Verkehrsmittel man eigentlich am Klimafreundlichsten reist und dies
zusammen mit Mathe verbunden.
Da der Verkehrssektor für rund 25% der CO2-Emissionen in
Europa verantwortlich ist und klimafreundliches Reisen dabei hilft die globale Erderwärmung zu
bremsen, habe ich mir dieses Thema für mein Projekt ausgesucht. Hierzu habe ich mir als erstes
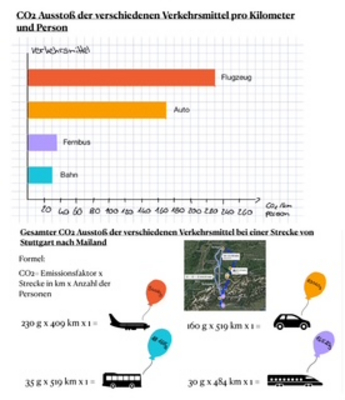
angeschaut wie viel CO2 die verschiedenen Verkehrsmittel (Flugzeug, Auto, Fernbus und Bahn) pro
Kilometer und Person ausstoßen. Darauf hin habe ich mir die Stecke Stuttgart nach Mailand
ausgesucht, für die ich die CO2-Emissionen berechnen wollte. Als Nächstes habe ich dann mithilfe
der Formel: Emissionsfaktor x Strecke in km x Anzahl der Personen, den CO2 Ausstoß für die
Strecke der verschiedenen Verkehrsmittel berechnet. Da ich mir dachte, dass es einfacher ist, wenn
man einfach nur die Kilometer Anzahl einer Strecke in ein Programm eingibt und dann direkt die
CO2-Emissionen der 4 Verkehrsmittel für diese Strecke angezeigt werden, habe ich mithilfe eines
Programmcodes genau so ein Programm geschrieben.
Hier finden Sie noch ein kurzes Video zu meinem Programm.
Celine Echle
Mathematik trifft Umwelt: Das stille Sterben der Bienen
Im Rahmen des Mathematikunterrichts habe ich mich mit der Frage beschäftigt, wie mathematische Modelle helfen können, die Auswirkungen von Umweltfaktoren auf Tierpopulationen darzustellen. Als konkretes Beispiel haben ich die Bienenpopulation in Baden-Württemberg analysiert, ein Thema, das nicht nur mathematisch interessant sondern auch ökologisch hochaktuell ist.
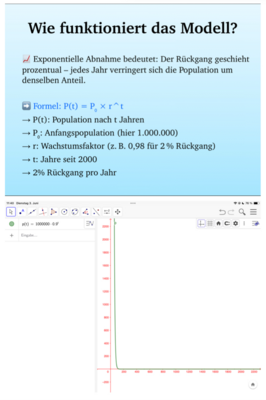
Der mathematische Teil: Modellierung mit GeoGebra
Um die Entwicklung der Bienenpopulation von 2000 bis 2025 zu untersuchen, habe ich reale Daten aus
wissenschaftlichen Quellen genutzt, wie die Rote Liste der LUBW und diese mithilfe der Software
GeoGebra grafisch dargestellt. So konnte ich nachvollziehen, wie sich die Anzahl der Bienenvölker in
Baden-Württemberg über die Jahre verändert hat und wie sich die Anzahl verändern könnte in den nächsten
25 Jahren.
Die grafische Darstellung zeigt deutlich:
• Einen langsamen Rückgang der Population in den frühen 2000er-Jahren.
• Jahr 2000: 1.000.000 Wildbienen (angenommen)
• Jahr 2025: ca. 603.000 → ~ 40 % Rückgang
• Jahr 2050: ca. 364.000→ ~ 63 % Rückgang
• In den letzten Jahren leichte Schwankungen, teils durch Maßnahmen zur Bienenschutzförderung, teils
durch weiterhin bestehende Umweltprobleme.
Nikola Witek
Mathematik in der Kunst
Als ich mit dem Thema angefangen hab, dachte ich: Kunst ist ja was cooles und kreatives aber Mathe ist… naja, halt Mathe. Zahlen, Formeln, Taschenrechner. Aber je mehr ich mich damit beschäftigt habe, desto klarer wurde: Mathe steckt überall in der Kunst. Und zwar nicht nur ein bisschen. Viele berühmte Künstler haben mathematische Prinzipien ganz bewusst genutzt, um ihre Werke zu planen, aufzubauen oder harmonisch wirken zu lassen. Leonardo da Vinci zum Beispiel war nicht nur Künstler, sondern auch Mathematik-Fan. Er benutzte den Goldenen Schnitt – ein ziemlich berühmtes Zahlenverhältnis, das als besonders ausgewogen empfunden wird. In seinen Zeichnungen und Gemälden achtete er darauf, dass wichtige Elemente genau nach diesem Prinzip angeordnet waren. Das sieht man zum Beispiel beim Mona lisa, aber auch in seinen Gemälden. Noch spannender wird’s bei M. C. Escher. Der hat Bilder gemalt, die aussehen, als wäre er in einer optischen Täuschung spazieren gegangen. Treppen, die im Kreis laufen, Muster, die sich endlos wiederholen. Seine Spezialität waren sogenannte Parkettierungen , also Muster, die sich ohne Lücken aneinanderfügen. Er nutzte Spiegelungen, Drehungen und mathematische Symmetrien, um seine Kunst zu gestalten. Und jetzt kommt das Beste: Ich hab’s selbst ausprobiert. Ich hab einen geometrischen Körper gebaut, genauer gesagt einen Ikosaeder – das ist ein Körper mit 20 gleichseitigen Dreiecken. Und darauf habe ich ein eigenes Fisch-Muster gemalt, das sich – ganz im Stil von Escher – symmetrisch wiederholt. Ich habe dabei mit Formen, Winkeln, Wiederholungen und Farben gearbeitet. Es war also gleichzeitig Mathe, Kunst und Bastelstunde in einem. Und ehrlich gesagt: Es hat richtig Spaß gemacht. Mein Fazit aus dem Ganzen? Künstler benutzen Mathe nicht, weil sie müssen, sondern weil sie damit bestimmte Wirkungen erzeugen können. Der Goldene Schnitt sorgt dafür, dass ein Bild ausgewogen wirkt. Geometrie und Symmetrie bringen Struktur und Klarheit ins Bild. Und Rasterlogik hilft dabei, Flächen sinnvoll aufzuteilen. Mathe ist in der Kunst also keine Einschränkung – sondern ein ziemlich geniales Werkzeug. Wer hätte gedacht, dass ausgerechnet Mathe dafür sorgt, dass Kunst so gut aussieht?
Rana Adel
Mathematik ist überall - ein Projekt der JS2 im Schuljahr 2023 / 2024
Im Mathematikkurs der Jahrgangsstufe 2 (erhöhtes Anforderungsniveau, Kurs: Frau Wellmann) haben 12 Schülerinnen umfassende Mathematikprojekte erarbeitet. Diese Projekte, die unterschiedliche mathematische Themen und Anwendungen behandeln, sind unten aufgeführt.
Mit Mathematik die Welt retten: Ein interaktives Abenteuer
Im Rahmen unseres Matheprojekts haben wir ein innovatives interaktives Spiel entwickelt, das Mathematik mit spannender Storytelling verbindet. Das Ziel ist es, Schülern auf eine unterhaltsame Weise mathematische Konzepte näherzubringen.
Das Spiel dreht sich um einen Protagonisten, den der Spieler selbst benennen kann. Der Held oder die Heldin taucht in einer fremden Welt auf und schließt sich einem Widerstand an, der gegen die Pläne eines bösen Professors und seiner KI-Assistenten kämpft. Der Spieler muss mathematische Aufgaben lösen, um den Widerstand zu unterstützen und die Pläne des Professors zu vereiteln. Das Spiel enthält Entscheidungspunkte, die auf mathematischen Aufgaben basieren und den Verlauf der Geschichte beeinflussen. Das Ende hängt von den mathematischen Fähigkeiten und Entscheidungen des Spielers ab.
Neben der Handlung gibt es Trainingsphasen, in denen die Spieler neue mathematische Regeln oder Themen üben. Diese Phasen bereiten die Spieler auf die Herausforderungen des Spiels vor. Die Spieler erhalten kontinuierlich Tipps und Hinweise, um auch bei Schwierigkeiten erfolgreich zu sein. Das Spiel ist für Einzelspieler konzipiert, sodass jeder individuell die Geschichte erleben kann.
Wir sind noch in der Entwicklungsphase, haben aber eine funktionierende Demo mit Python erstellt. Diese Demo zeigt die grundlegende Mechanik des Spiels und die Integration der mathematischen Herausforderungen. Unser interaktives Spiel kombiniert Mathematik mit spannender Handlung und fördert die mathematischen Fähigkeiten der Spieler. Die Python-Demo markiert einen wichtigen Schritt und uns hat es Spaß gemacht, dieses Projekt machen zu können.
Während der Entwicklung standen wir vor der Herausforderung, die komplexe Handlung des Spiels mit den interaktiven mathematischen Elementen nahtlos zu verbinden. Aufgrund technischer und zeitlicher Beschränkungen konnten wir diese Integration nicht vollständig umsetzen. Um dennoch den Schwierigkeitsgrad und die verschiedenen mathematischen Herausforderungen des Spiels zu veranschaulichen, haben wir zwei separate kleine Spiele entwickelt.
Hier finden Sie den Programmcode.
Hier finden Sie einen kurzen Trailer zum Spiel.
Ein Projekt von Carla und Jennifer.
Analysis und Modellieren
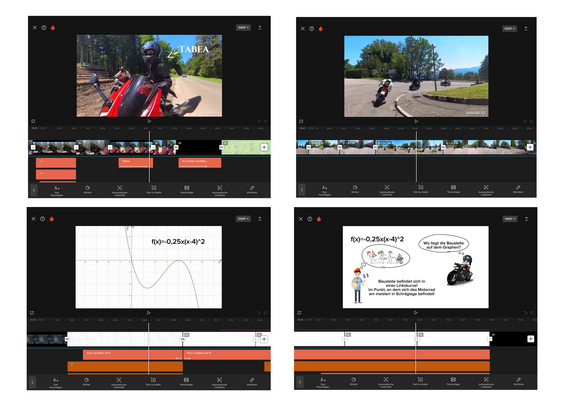
Für mein Projekt habe ich mir überlegt zwei meiner Hobbys miteinzubeziehen: Das Motorradfahren und der Videoschnitt.
Um den Bezug zu Mathe herzustellen, habe ich mir eine Story überlegt. Diese handelt von vier Freunden, die zusammen Motorrad fahren gehen. Ihre Fahrtstrecke lässt sich mit einer Funktion beschreiben. Auf ihrer Strecke erhalten sie Informationen über Hindernisse auf der Straße. Den genauen Ort müssen die Freunde dann ausrechnen.
Das Ziel des Projektes ist es, den Zuschauern das Modellieren anschaulich näherzubringen und gleichzeitig auch für Unterhaltung zu sorgen.
Einen kleinen Ausschnitt meines Projektes können Sie sich hier ansehen.
Ein Projekt von Tabea.
Mathe leicht gemacht mit Rechenhilfsprogrammen
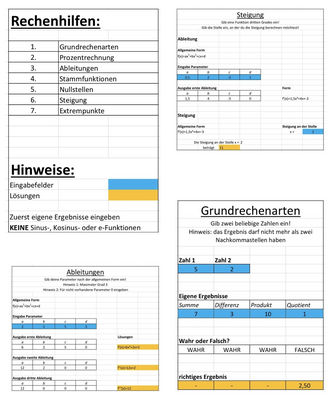
Mathematik kann manchmal ganz schön schwierig sein. Deshalb haben wir Rechenhilfen für verschiedene mathematische Probleme entwickelt. Sie sind für Schülerinnen und Schüler verschiedener Jahrgangsstufen geeignet.
Besonders für Grundschüler eignet sich das Grundrechenarten-Programm, um selbstständig die eigenen (Haus-)Aufgaben zu kontrollieren. Das Prozentrechen-Programm ist eher für die Unterstufe gedacht. Auch Ableitungen und Stammfunktionen werden von dem Programm ganz leicht berechnet. Nullstellen-, Steigung- und Extrempunktberechnung funktioniert mit dem Programm ganz schnell.
Bei all diesen Aufgaben muss einfach nur die Ausgangsfunktion eingegeben werden. Einige der Programme sind eher zum Überprüfen der eigenen Ergebnisse gedacht, andere eher zum Rechnen. Mit diesen Programmen wird Mathe für alle leichter und macht mehr Spaß.
Hier finden Sie die zugehörige Exceldatei.
Ein Projekt von Emily, Enya und Samira.
Grundschulkinder Mathe erklären
In unserem Projekt zeigen wir, wie man Kindern aus der Perspektive eines Lehrers Mathematik verständlich beibringen kann und welche Methoden und Grundlagen dabei hilfreich sind. Wir haben uns auf das Additionsverfahren spezialisiert und zusätzlich Mathe-Spiele gebastelt, um zu demonstrieren, wie man das Addieren spielerisch mit den Kindern üben kann.
Um am besten das Additionsverfahren erklären zu können, haben wir uns auf die Grundvorstellungen und die Darstellungsformen fokussiert.
Für unsere gebastelten Spiele entschieden wir uns für drei Übungsspiele und ein Hilfsmittel. Das erste Übungsspiel nannten wir "Rechnen mit Händen", bei dem Kinder verschiedene Rechenaufgaben erstellen und dabei ihre Hände zur Hilfe nehmen können. Das zweite Spiel heißt "Rechnen nach Drehen"; durch das Rotieren der Becher entstehen immer neue Rechnungen, die die Kinder zum Üben nutzen können. Das letzte Spiel ist "Autorennen". Hier können drei Kinder einen Wettbewerb durchführen, bei dem sie für jede richtig gelöste Aufgabe einen Schritt weiterfahren dürfen. Der Sieger erhält am Ende einen Preis. Schließlich bastelten wir ein Hilfsmittel, mit dem die Kinder ihre Aufgaben kontrollieren können: eine einfache Tabelle des Einmaleins.
Ein Projekt von Ariane und Ghris.
Malen nach Mathebasics
Die einfache Form von Malen nach Zahlen kennen die Meisten. Unser Projekt ist eine erweiterte Form hiervon, die im Unterricht der Vertiefung von Mathe-Basics dienen soll und gleichzeitig Abwechslung vom oft eher eintönigen Unterricht bietet.
Unser Ziel ist es, den Schüler*innen zu zeigen, dass Lernen Spaß machen kann und sie dadurch gerne zur Schule gehen.
Wir haben Bilder für unterschiedliche Klassenstufen erstellt, sodass von Kindergarten bis Oberstufe alle Altersklassen abgedeckt sind.
Das Anforderungsniveau steigert sich von einfachen Zahlen, die lediglich verbunden werden müssen, über Additions-, Subtraktions-, Multiplikations- und Divisionsrechnungen, bis hin zu Aufgaben mit Brüchen, Wurzelziehen, Quadratzahlen und Ableitungsfunktionen.
In dem nebenstehenden Bild ist beispielsweise eine Ausführung unseres Projekts mit Ableitungsfunktionen und eine weitere mit Additions-, Subtraktions-, Multiplikations- und Divisionsrechnungen zu sehen.
Ein Projekt von Alena und Jessica.
Mathematik in der Ernährung
Mit meiner Ausarbeitung möchte ich diejenigen unter euch ansprechen, die gerne Mathe machen aber keinen Plan von Ernährung haben. Ich habe fünf konkrete Beispiele ausgearbeitet, an denen ihr erkennen könnt, dass Ernährung nicht ohne Mathe funktioniert.
Als erstes Beispiel der BMI. Der Body Mass Index (BMI) ist ein Gesundheitsmaßstab, der individuell für jeden berechnet wird. Um schauen zu können, ob man mit seinem Gewicht in dem Normalbereich liegt, eignen sich Zahlen besonders gut als Vergleichsmedium.
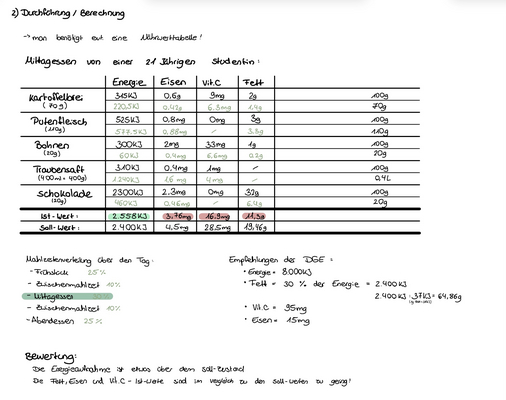
Um weitere Beispiele anzuführen, wäre da noch die Nährwertberechnung, die Berechnung des Tageskostplans, die Berechnung mit Alkoholwerten oder die Gesamtenergiebedarfsberechnung.
Nebenstehend ist ein Ausschnitt aus meiner Ausarbeitung zum Thema Tageskostplanberechnung!
Ein Projekt von Jana.
Normative Modellierung und Wahlen – oder: Wie Mathematik unsere Politik beeinflusst


Was zu Beginn wie der Albtraum vieler Schüler klang, entpuppte sich bei genauerem Hinsehen als spannendes Projekt der Lehrerinnen Frau Wellmann und Frau Mühlberger, die die Schülerinnen und Schüler der BTG1/2 und der EG1 an die Schnittstelle von Wahlen und Mathematik führten. Die normative Modellierung wirkt sich über verschiedene Wahlsysteme direkt auf unser politisches Geschehen aus. Nachdem die Klassen das Verfahren nach Niemeyer und seine Stärken und Schwächen am Beispiel einer fiktiven Entenhausener Wahl, bei der die Schülerinnen und Schüler die Bürger darstellten, errechnet hatten, stellte sich natürlich die Frage, welche anderen Möglichkeiten einer Wahldurchführung es gäbe – an dieser Stelle traten Sainte Laguë und d´Hondt auf den Plan. Die beiden Wahlsysteme, die die Grundlagen sowohl für die Problematik der Parteienzersplitterung des Weimarer Reichstags als auch für die Vormachtstellung der Volksparteien während langer Jahrzehnte der bundesrepublikanischen Geschichte bilden, brachten die Köpfe zum Rauchen und die Diskussionen zum Glühen. Diskutiert wurde hierbei darüber, ob die Systeme, die mathematisch alle korrekt sind, auch gerecht sind oder ob kleinere oder größere Parteien unterschiedliche Wahlsysteme bevorzugen könnten. Abschließend wurde die Rückkehr zum Verfahren nach Sainte Laguë 2008 mit den aktuellen Modifikationen und ihren Auswirkungen auf die Zusammensetzung des Bundestags diskutiert, wobei auch die aktuelle Wahlrechtsreform nicht außer Acht gelassen wurde.
Unser Fazit: Jede Stimme zählt, denn auch die dritte Nachkommastelle kann bei der Auszählung der Stimmen zu einem Sitz im Bundestag führen!
An dieser Stelle ergeht eine Danksagung an die Studierenden des KIT Sarah Glatt und Beatrice Wellmann, die die Grundlagen und viele der Materialien lieferten.
Mathematik-Unterricht in den neuen Eingangsklassen - Einblicke in eine Unterrichtsstunde
Bild 1: „Kreative Darstellung einer Funktion“
Die Kreativität soll auch im Mathematikunterricht nicht zu kurz kommen! Der Arbeitsauftrag an die Schülerinnen und Schüler lautete: „Du hast 60 Sekunden Zeit. Stelle eine von dir gewählte mathematische Funktion mit Gegenständen deiner Wahl (eigener Körper, Tablet, Materialien aus dem Mäppchen etc.) dar!“
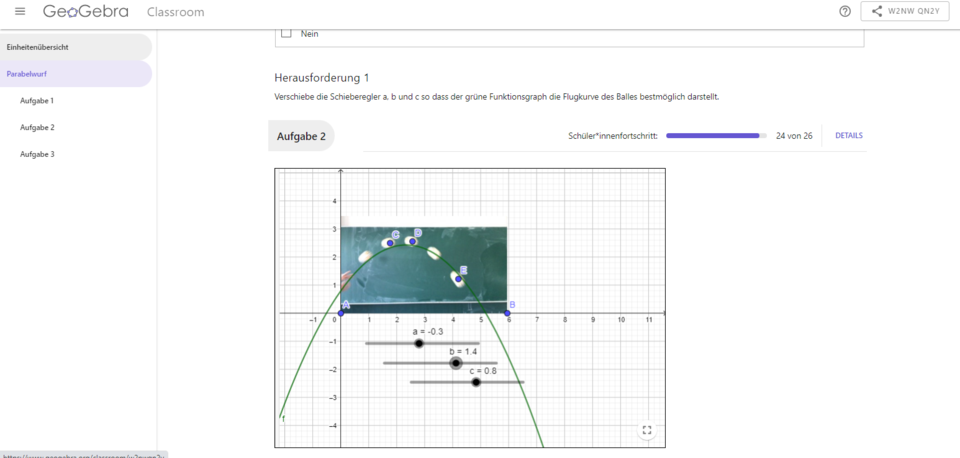
Bild 2: „Parabelwurf – Quadratische Funktion“
Mathematik findet sich im Alltag fast immer wieder! Nachdem im Unterricht ein Ball geworfen wurde, konnten die Schülerinnen und Schüler daraufhin die dargestellte GeoGebra Aufgabe mit ihrem Tablet bearbeiten. Der Parabelwurf stellt eine Alltagssituation dar, welche durch eine Parabel dargestellt werden kann.

Bild 3: „Spiel: Termumformungen“
Mathematikunterricht soll Spaß machen – nicht nur für gute Schüler*innen! Bei diesem Spiel arbeiten die Schülerinnen und Schüler in Kleingruppen und versuchen Fragen zu Termen richtig zu beantworten. Das Schwierigkeitsniveau einer Frage (einfach, mittel und schwer) kann selbst gewählt werden und das zusätzliche Würfeln ermöglicht auch schwächeren Schüler*innen zu gewinnen.
Tablet-Einsatz im Mathematik-Unterricht


Die Klassen der gymnasialen Oberstufe sind komplett mit iPads ausgestattet, die eine digitale Heftführung ermöglichen. Dazu verwenden die Schüler*innen Notability oder GoodNotes. Die Vorteile der digitalen Heftführung sind unter anderem das Einbinden von weiterem Material (z.B. Bilder, mathematische Zeichnungen, Arbeitsblätter, usw.), das schnelle Korrigieren und das nachträgliche Überarbeiten von Heftaufschrieben. Zudem steht den Schüler*innen sämtliches Arbeitsmaterial auf Moodle jederzeit zur Verfügung, das einerseits leicht in das digitale Heft eingebunden werden kann und andererseits eine ressourcenschonende Möglichkeit darstellt, die viel Papier einspart. Verlorene Arbeitsblätter gehören somit der Vergangenheit an, da diese jederzeit erneut heruntergeladen werden können.
Auch der Austausch von den Ergebnissen einer Gruppenarbeit ist papierlos über AirDrop schnell und einfach möglich. Die zu einem Vortrag erstellten Handouts können vor, während oder nach der Stunde zügig ausgeteilt werden, ohne dass in den Pausen unter Stress die Kopien für die Klasse angefertigt werden müssen. Sollte sich doch mal ein Fehler in der Ausfertigung eingeschlichen haben, kann dieser vor Ort korrigiert und eine aktuelle Version verteilt werden.
Buch vergessen? Kein Problem. Die entsprechende Seite wird abfotografiert und nach Beenden der Aufgabe wieder gelöscht. So wird unnötiger Datenmüll vermieden und das Urheberrecht gewahrt.
Komplett papierlos? Natürlich nicht. Es wird weiterhin mit Büchern und Arbeitsheften gearbeitet. Auch das Schreiben auf Papier darf nicht „verlernt“ werden, da sämtliche Leistungsnachweise nach wie vor schriftlich auf Papier zu erfolgen haben. Das heißt: iPads sind aktuell eine sinnvolle Ergänzung.
Neben der digitalen Heftführung ermöglichen die iPads auch die Verwendung von einer Vielzahl an sinnvollen Apps, die den Unterricht in unterschiedlicher Art und Weise unterstützen. Eine davon ist GeoGebra. Mit GeoGebra classic lassen sich die Graphen von Funktionen einfach zeichnen, wodurch die App eine Kontrollmöglichkeit für Schüler*innen darstellt. Weiterhin ist es möglich Ideen in der Erarbeitungsphase schnell und einfach auszuprobieren, wodurch die Motivation und der Spaß am Fach steigt. Die Schüler*innen lernen diese App auf unterschiedlichste Weise zu nutzen und damit Funktionsgraphen in Abhängigkeiten von Parametern zu verstehen und zu analysieren. Die Ergebnisse können dann durch Einbinden ins digitale Heft gesichert werden.
Weiterführende Links zu diversen Mathematik-Websites
GeoGebra - classic:
GeoGebra classic bietet die Möglichkeit beliebige Funktionen zu zeichnen und zu analysieren. Nachfolgend sind ein paar Aufgabentypen aufgelistet, bei denen GeoGebra classic in der Oberstufe weiterhilft:
- Funktionsgraphen zeichnen
- Schnittpunkte zweier Graphen bestimmen
- Nullstellen bestimmen
- Extrempunkte bestimmen
- Ableiten und integrieren
- Flächenberechnung mittels Integralrechnung
Du kannst dieses Programm auf jedem Endgerät nutzen.
Teste gleich hier, ob dir GeoGebra classic gefällt.
Aufgabenfuchs:
Hier gibt es zahlreiche Übungsaufgaben zu verschiedenen Themen, wie bspw.:
- Kopfrechnen
- Gleichungen lösen
- Potenzen berechnen
- lineare und quadratische Funktionen
Viel Spaß und Erfolg beim Üben und Wiederholen.
Super-Mario:
Wird ein Gegenstand geworfen, so kann die Flugbahn dieses Gegenstands näherungsweise als Parabel beschrieben werden. Auch der Sprung von Super-Mario hat das Aussehen einer Parabel. Parabeln sind also vielfältig und machen Spaß!
Du bist noch nicht überzeugt? Dann versuche es selbst und sammel mit Super-Mario möglichst viele Sterne.